CFC数据结构与算法训练指南题解（五）

A – Intersecting Lines

A题：判断两直线是否相交

• 输入： 第一行包含一个介于1和10之间的整数N，表示有多少对直线。接下来的N行将各包含八个整数。这些整数表示平面上四个点的坐标，顺序为x1 y1 x2 y2 x3 y3 x4 y4，每个数字由空格隔开。他们表示平面上分别过前两点和后两点的两条直线:穿过(x1，y1)和(x2，y2)的线和穿过(x3，y3)和(x4，y4)的线。点(x1，y1)总是不同于(x2，y2)。(x3，y3)和(x4，y4)也是如此。
• 输出： 有N+2行输出。输出的第一行应为“INTERSECTING LINES OUTPUT”。然后每对直线按顺序依次输出一行，描述这对直线的关系:无相交点（NONE）、相交于线（LINE）或相交于点。如果相交于点，那么你的程序应该输出该点的x和y坐标，精确到小数点后两位（例：POINT 2.00 2.00）。输出的最后一行应为 “END OF OUTPUT”。

思路：

首先读取N的值，作为判断依据设置循环，再循环读取每对直线的数据，根据公式判断两直线关系。相交条件： k1!=k2 （k为斜率）；重合条件：k1==k2且 a1c2-a2c1==0&&b1c2-b2c1==0 （标准式系数）。

相关资料：

 

斜率k计算公式：标准式及系数计算公式：

交点坐标计算公式：

 

需要注意的是，当x2=x1时，k=1、x和y存在的前提是两直线相交。

B – Area

B题：求多边形面积

• 输入： 第一行输入是整数t(1≤t≤20)，即测试多边形的数量。以下每一行都包含一个由数字1-9组成的字符串，描述多边形是如何从原点开始走来形成的。这里，8、2、6和4代表北、南、东和西，而9、7、3和1分别代表东北、西北、东南和西南。数字5只出现在序列的末尾，表示停止行走。您可以假设输入多边形是有效的，这意味着端点始终是起点，多边形的边不互相交叉。每行最多可包含1000000位数字。
• 输出： 对于每个多边形，在一条线上打印其面积。

思路：

​ 因为此题的前提是从原点开始走，所以我们可以用叉积来计算其面积。即把该多边形分为多个三角形，例如图中P0P1P2构成一个三角形，所有三角形的面积之和即为该多边形的面积，需要注意的是考虑到凹多边形的情况，计算小三角形面积不应取绝对值，最后的结果是所有三角形面积先相加再取绝对值。

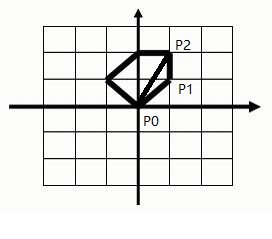
先记录t作为循环判断条件来设置循环，再读取走的方向，根据方向记录下当前顶点和前一个顶点（p[1]，p[2]），注意用来记录顶点的两个值需要初始化为（0,0），每记录一次p[1]计算p[1]和p[2]以及p[0]（原点）组成的三角形面积，并加到总面积中，然后再更新p[2]（p[2]=p[1]），再次读取下一步方向，直到结束，最后取绝对值输出总面积。

相关资料：

– 注意：本题由于精度问题不能使用double，而int会超出范围，要用long long。

C – Wall

C题：凸包周长

• 输入： 输入文件的第一行包含由空格分隔的两个整数。N (3 <= N <= 1000)是国王城堡中的顶点数，而L (1 <= L <= 1000)是国王允许墙壁接近城堡的最小英尺数。 接下来的N条线以顺时针顺序描述城堡顶点的坐标。每行包含两个整数Xi和Yi (-10000 <= Xi，Yi < = 10000)，用一个空格隔开，表示第i个顶点的坐标。所有顶点都是不同的，城堡的侧面除了顶点之外没有相交的地方。
• 输出： 向输出文件中写入一个数字，该数字代表城堡周围为满足国王的要求而建造的最小长度(英尺)。你必须向国王展示整数英尺，因为浮点数还没有发明出来。但是，您必须以这样的方式对结果进行舍入，使其精确到8英寸(1英尺等于12英寸)，因为国王不会容忍估算中出现更大的误差。 （四舍五入即可）。

思路：

​ 本题在求解凸包的基础上作了要求：城墙要距离城堡至少L英尺。城墙长度等于求出来的凸包周长再加上一个半径为L的圆形的周长，我们可以通过下图证明：

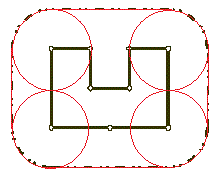
快包：S为城堡顶点的集合，我们把这些点按x的升序排序，如果x相同则按y的升序排序，则易证P1和Pn为该集合的左右顶点，以P1Pn为直线，把该集合里的点分为两个集合：S1是位于直线左侧或者在直线上的点的集合，S2是位于直线右侧或者在直线上的点的集合凸包边界由上下两条界限构成的，我们称为上包和下包。以上包为例，如果S1为空，则上包就是以P1和Pn为端点的线段，如果S1不空，则找到S1中距离直线P1Pn最远的点Pmax，如果有多个这样的点，则选让∠PmaxP1Pn最大的点，然后找出所有在S1中所有在直线P1Pmax左边的点和Pmax以P1构成集合S1.1,左边的点和Pmax以Pn构成S1.2,则:

1. Pmax为上包的顶点。
2. 在△P1PmaxPn之中的点不可能是上包的顶点。
3. 不存在同时位于P1Pmax和PmaxPn两条直线左边的点

所有在利用递归继续构造上包，然后把它接起来，就可以得到整个集合的上包。

相关资料：

P1(x1,y1），P2(x2,y2），Pmax（x3,y3）使得这个三角形的面积最大，当S为正时，P（x3,y3)位于直线P1P2左侧。