第一题 图像渲染
题目简述:
给出一个整数构成的二维数组。每一个整数表示该图画的像素值大小,数值在 0 到 65535 之间。给你一个坐标 (sr, sc) 表示图像渲染开始的像素值(行 ,列)和一个新的颜色值 newColor,让你重新上色这幅图像。上色标准是从初始坐标开始,记录初始坐标的上下左右四个方向上像素值与初始坐标相同的相连像素点,接着再记录这四个方向上符合条件的像素点与他们对应四个方向上像素值与初始坐标相同的相连像素点,重复该过程。将所有有记录的像素点的颜色值改为新的颜色值。最后返回这个二维数组。
解析:
题目的意图很明显,从起点开始遍历图,找到符合条件的格子,重新赋值,直接考虑深度优先搜索或广度优先搜索即可。
DFS代码:
var floodFill = function (image, sr, sc, newColor) {
// 注意起点也需要染色
var startColor = image[sr][sc]
image[sr][sc] = newColor
// 四个方向的数组,方便dfs时循环上下左右四个方向
const dir = [[-1, 0], [0, 1], [1, 0], [0, -1]]
// 创建一个访问数组,以免重复访问一个格子,数组同image等大,0代表未访问,1代表已经访问过
var vis = new Array(image.length)
for (let i = 0; i < image.length; i++) {
vis[i] = new Array(image[0].length).fill(0)
}
// dfs
function dfs(x, y) {
vis[x][y] = 1 // 将这个格子置为已访问
for (let i = 0; i < 4; i++) { // 遍历四个方向
const nextX = x + dir[i][0]
const nextY = y + dir[i][1]
// 首先判断下一个方向是否越界,然后判断是否访问过,再判断是否与起点的值相同
if (nextX >= 0 && nextX < image.length && nextY >= 0 && nextY < image[0].length && vis[nextX][nextY] == 0 && image[nextX][nextY] == startColor) {
// 若以上条件都满足,则将这一格重新赋值,并以下一格为起点继续搜索
image[nextX][nextY] = newColor
dfs(nextX, nextY)
}
}
}
dfs(sr, sc)
return image
}
第二题 克隆图
题目简述:
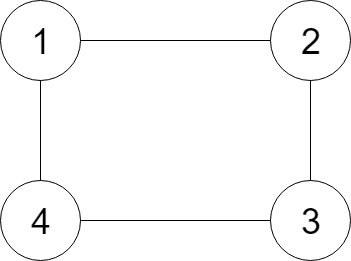
给定一个无向连通图的引用,返回这个引用的深拷贝,图中的每个节点都包含它的值 val(Int) 和其邻居的列表(list[Node])。
解析:
为了实现图的深度拷贝,我们需要遍历整张图,创建相应的节点,再按照原来的连接规则,连接我们创建的新的节点。这里我们考虑用DFS来遍历整张图,搜索节点。在遍历的过程中,去重是少不了的步骤,这个题里,我们需要在遍历的时候排除已经被创建的节点,因为我们需要搜索到新的节点,并创建它,已经被创建的节点直接使用就好了。我们考虑使用Map来判断这个值对应的节点是否已经被创建。
代码实现:
var cloneGraph = function(node) {
var map = new Map()
function dfs(input) {
// 这个节点值对应的点是否已经被创建,如果有,直接返回
if (map.get(input.val)) {
return map.get(input.val)
}
// 如果没有就创建这个点
var clone = new Node(input.val, [])
// 把它加入map中
map.set(clone.val, clone)
// 遍历这个点的邻节点,全部加入我们新创建的节点中
for (item in input.neighbors) {
// 这里其实就可以把dfs理解为“克隆一个输入的节点”这里就把所有邻节
// 点复制后加入到这次创建节点的邻节点中去
clone.neighbors.push(dfs(input.neighbors[item]))
}
// 返回这个已经创建好的节点
return clone
}
// 可以把dfs想象成一个复制函数,递归进行复制
return dfs(node)
}
第三题 删除无效的括号
题目简述:
删除最少的括号使得输入的括号字符串变得有效。
解析:
当我们看到删除最少的括号时,就要想到在DFS和BFS中,BFS是很适合这种有最少(短)思想的题目的,所以我们这个题首先考虑BFS。在删除括号的时候,如何判断本次得到有效括号是删除了最少的括号呢?这里有两种思路。
- 一、利用BFS的特性,在第一次得到有效括号串的时候,说明这次的括号删除是最少的,那么,后续,只将和本次删除括号数量相同的过程得到的有效结果加入答案列表。
- 二、事先对输入串进行处理,找出所有多余的左括号和右括号的数量,在得到有效结果的同时,判断本次删除的括号数量是否等于多余的括号之和
然后我们同样使用Map来进行去重,对已经产生判断过的括号串进行跳过。
代码实现:
class Solution {
public List<String> removeInvalidParentheses(String s) {
// 存放答案的列表
List<String> ans = new LinkedList<>();
// 注释部分是第二种判断方式的实现
// int left=0,right=0; // 左多余的括号 右多余的括号
// for(int i=0;i<s.length();i++){
// if(s.charAt(i)=='(')
// left++;
// else if(s.charAt(i)==')'){
// if(left>0)
// left--;
// else
// right++;
// }
// }
int len = 0; // 记录第一次出现的有效串时删除的长度
// bfs的辅助队列,每次得到无效串就加入到队列
Queue<String> que = new LinkedList<>();
// 用于去重的map
Map<String,Integer> vis = new HashMap<>();
vis.put(s,1); // 首先将输入串标记为访问过
que.offer(s); // 输入串作为队列第一个处理项
// 以下为BFS标准处理流程
while(!que.isEmpty()){
String temp = que.poll();
// 第一种判断方式
if(isVailid(temp)){
if(ans.size() == 0) { // 如果这是第一个答案
// 记录下这次删除的长度
len = s.length() - temp.length();
ans.add(temp);
} else {
// 后续得到的答案需要判断删除的长度
if (s.length() - temp.length() == len) {
ans.add(temp);
}
}
continue;
}
// 第二种判断方式
// if(isVailid(temp)){
// if(temp.length()==s.length()-(left+right))
// ans.add(temp);
// continue;
// }
for(int i=0;i<temp.length();i++){
// 跳过不是括号的字符
if(temp.charAt(i)!='('&&temp.charAt(i)!=')')
continue;
String str = temp.substring(0,i)+temp.substring(i+1);
// 如果得到的串没有被访问过,加入队列并且标记访问
if(vis.get(str)==null){
que.offer(str);
vis.put(str,1);
}
}
}
return ans;
}
// 判断串是否合法
boolean isVailid(String s){
int sum=0;
for(int i=0;i<s.length();i++){
if(s.charAt(i)=='(')
sum++;
else if(s.charAt(i)==')'){
sum--;
// 若统计值为负了,说明右括号多余,已经不可能闭合,则直接返回不合法
if(sum<0)
return false;
}
}
return sum==0;
}
}