最近在研究无锁跳表,无意间发现了这篇论文,虽然是有锁的实现,但是采用了乐观同步的机制,是一个理论上简单且高效的并发安全的跳表实现。苦于国内网上少有针对此篇论文的翻译与解读,本篇博客致力于翻译此篇论文,并基于 zhangyunhao116/skipmap 的开源代码逻辑,深入理解篇论文的思想。
论文原文:
https://people.csail.mit.edu/shanir/publications/LazySkipList.pdf
论文翻译
摘要
由于跳跃表具有高度分布式的特性和缺乏全局再平衡机制,它们正在成为并发应用中越来越重要的对数搜索结构。不幸的是,文献中的并发跳跃表实现,无论是基于锁还是无锁的,都没有被证明是正确的。此外,这些算法的复杂结构很可能是缺乏证明的原因,也给希望扩展和修改算法或在其基础上构建新结构的软件设计人员带来了障碍。
本文提出了一种简单的基于锁的并发跳跃表算法。与其他并发跳跃表算法不同,该算法始终保持跳跃表的性质,便于推理其正确性。尽管它是基于锁的,但该算法通过一种新颖的乐观同步方式实现了高度的可扩展性:在添加或删除节点之前,它在不获取锁的情况下进行搜索,仅需要进行短暂的基于锁的验证。实验证据表明,在最常见的搜索结构使用模式下,这种更简单的算法与已知的最佳无锁算法的性能相当。
1 引言
跳跃表(Skip-lists)^[11]^是一种越来越重要的数据结构,用于存储和检索有序的内存中数据。在本文中,我们提出了一种新的基于锁的并发跳跃表算法,该算法在大多数常见的使用条件下似乎与现有的最佳并发跳跃表实现表现相当。我们实现的主要优点在于它更简单,更易于推理。
Pugh^[10]^提出的原始基于锁的并发跳跃表实现由于使用指针反转而变得相当复杂,据我们所知,尚未证明其正确性。Doug Lea^[8]^根据Fraser和Harris^[2]^的工作编写的ConcurrentSkipListMap,并作为Java SE 6平台的一部分发布,是我们所知的最有效的并发跳跃表实现。该算法是无锁的,并且在实践中表现良好。这种实现的主要限制在于它过于复杂。某些交错操作可能导致通常的跳跃表不变式被违反,有时是暂时性的,有时是永久性的。这些违规似乎不会影响性能或正确性,但它们使得很难推理算法的正确性。相比之下,此处介绍的算法基于锁,并且始终保持跳跃表的不变性。该算法足够简单,我们能够提供直接的正确性证明。
我们的新颖基于锁的算法的关键是两种互补的技术的结合。首先,它是乐观的:方法在不获取锁的情况下遍历列表。此外,在遍历列表时,它们可以忽略其他线程获取的锁。只有当方法发现所需的项时,才会锁定该项及其前驱,并验证列表是否未更改。其次,我们的算法是延迟的:删除项涉及在物理上将其移除(取消链接)之前,通过标记逻辑上删除它。
Lea^[7]^观察到最常见的搜索结构使用模式中,搜索操作明显占主导地位,插入操作占主导地位,而删除操作占很小比例。一个典型的模式是90%的搜索操作,9%的插入操作和仅有1%的删除操作(参见^[3]^)。在Sun Fire T2000多核和Sun Enterprise 6500上进行的初步实验测试表明,尽管我们新的乐观基于锁的算法非常简单,但在这种常见的使用模式下,它的性能与Lea的ConcurrentSkipListMap算法相当。实际上,只有在多程序环境中出现极端争用的不常见条件下,我们的新算法才比ConcurrentSkipListMap算法表现更好。这是因为我们的原始实验实现没有添加任何争用控制。
因此,我们相信在需要理解并可能修改基本跳跃表结构的应用程序中,所提出的算法可能是ConcurrentSkipListMap算法的一个可行替代方案。
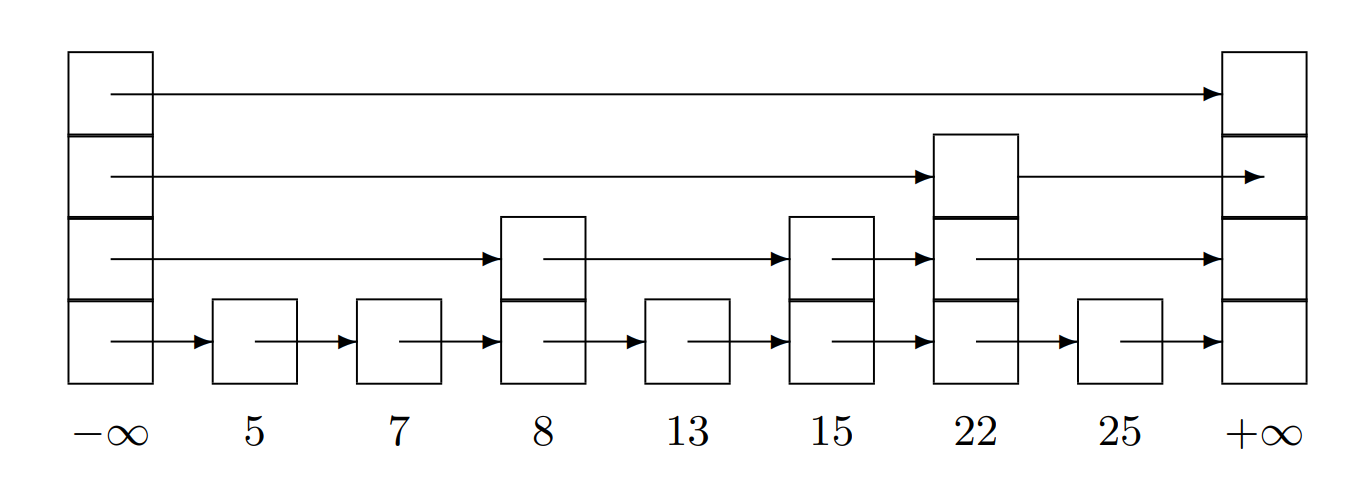
Figure 1: 一个最大高度为4的跳表。每个节点下方的数字(即next指针数组)是该节点的键,其中左侧哨兵节点的键为-∞,右侧哨兵节点的键为+∞。
2 背景
跳跃表(Skip-list)^[11]^是一种按键排序的链表。每个节点被分配一个随机的高度,高度最大值有限。在任何一个高度上的节点数以指数方式减少。跳跃表节点在每个高度上都有一个后继节点。例如,一个高度为3的节点有三个下一个指针,一个指向高度为1的下一个节点,另一个指向高度为2的下一个节点,依此类推。图1显示了一个带有整数键的跳跃表。
我们将跳跃表看作具有多个层次的列表,并且我们讨论每个层次上节点的前驱和后继。除了底层之外,每个层次上的列表是下一层级列表的子列表。由于更高的高度上节点的数量指数级减少,因此我们可以通过首先在较高的层次上进行搜索来快速找到键,跳过较短节点的大量数量,并逐渐向下工作,直到找到具有所需键的节点,或者到达底层。因此,跳跃表操作的期望时间复杂度是列表长度的对数。
在列表的开始和结束处,有左哨兵和右哨兵节点,这样比较方便。这些节点具有最大的高度,当跳跃表为空时,右哨兵在每个层次上都是左哨兵的后继节点。左哨兵的键值比任何可能添加到集合中的键都要小,而右哨兵的键值比任何可能添加到集合中的键都要大。因此,搜索跳跃表始终从左哨兵开始。
class Node {
int key;
int topLayer;
Node ∗∗ nexts;
bool marked;
bool fullyLinked;
Lock lock;
}
Figure 2: A node
3 我们的算法
我们在支持三个方法的集合对象的实现的背景下介绍我们的并发跳跃表算法,这三个方法是add、remove和contains:add(v)将v添加到集合中,并且当v不在集合中时返回true;remove(v)从集合中删除v,并且当v在集合中时返回true;contains(v)当v在集合中时返回true。我们展示了我们的实现是可线性化的^[6]^,也就是说,每个操作似乎在其调用和响应之间的某个点(线性化点)上以原子方式执行。我们还展示了该实现是无死锁的,并且contains操作是无等待的;也就是说,只要线程不停地执行步骤,它就保证能完成contains操作,而不受其他线程活动的影响。
我们的算法建立在Heller等人的懒惰列表算法^[4]^基础上,这是一个简单的并发链表算法,其add和remove操作使用乐观细粒度锁定机制,而contains操作是无等待的:我们在跳跃表的每个层次上使用懒惰列表。与懒惰列表一样,每个节点的Key严格大于其前驱节点的Key,并且每个节点都有一个标记标志,用于使remove操作看起来是原子的。然而,与简单的懒惰列表不同,我们可能需要在多个层次上链接节点,因此可能无法通过单个原子指令插入节点,该指令可以作为成功添加操作的线性化点。因此,在懒惰跳跃表中,我们为每个节点添加了一个额外的标志fullyLinked,在节点在所有层次上都被链接之后将其设置为true;设置此标志是我们跳跃表实现中成功添加操作的线性化点。图2显示了一个节点的字段。
如果且仅当列表中存在一个未标记、完全链接的具有该Key的节点时(即从左哨兵可达),Key就在抽象集合中。
为了维护跳跃表的不变性,即每个列表都是较低层次列表的子列表,在对需要修改的所有节点获取锁时才会对列表结构(即next指针)进行更改。(有一个例外是涉及添加操作的规则,稍后讨论。)
在对算法的下面详细描述中,我们假设存在垃圾收集器来回收从跳跃表中删除的节点,因此在任何线程可能仍然访问这些节点时,删除的节点不会被重新利用。在证明(第4节)中,我们假设节点永远不会被重新利用。在没有垃圾回收的编程环境中,我们可以使用解决重复使用问题的解决方案^[5]^或危险指针[hazard pointers] ^[9]^来实现相同的效果。我们还假设Key是从MinInt+1到MaxInt-1的整数。我们使用MinInt和MaxInt作为LSentinel和RSentinel的Key,它们分别是左哨兵和右哨兵节点。
在跳跃表中进行搜索是通过findNode辅助函数完成的(见图3),该函数接受一个键v和两个最大高度的节点指针数组preds和succs,并且与顺序跳跃表完全一样进行搜索,从最高层开始,每次遇到大于或等于v的节点时向下一个更低的层继续搜索。线程在preds数组中记录了在每个层次上遇到的最后一个键小于v的节点及其后继节点(后继节点的键必须大于或等于v)。如果找到具有所需Key的节点,findNode返回找到此类节点的第一个层次的索引;否则,返回-1。为了简化演示,即使在更高层次找到具有所需键的节点,findNode也会继续执行到底层,因此在findNode终止后,preds数组和succs数组中的所有条目都被填充(请参见第3.4节,了解实际实现中使用的优化)。请注意,findNode不获取任何锁,也不会在出现与其他线程冲突的访问时进行重试。现在我们逐个考虑每个操作。
int findNode( int v, Node∗ preds[], Node∗ succs[]) {
int lFound = -1;
Node∗ pred = &LSentinel ;
for(int layer = MaxHeight −1; layer ≥ 0; layer−−){
Node∗ curr = pred −> nexts[layer];
while(v > curr−>key) {
pred = curr;
curr = pred−>nexts[layer];
}
if(lFound == −1 && v == curr −> key){
lFound = layer;
}
preds[layer] = pred;
succs [layer] = curr;
}
return lFound;
}
Figure 3: The findNode helper function
3.1 添加操作
添加操作(见图4)调用findNode函数来确定列表中是否已存在具有该键的节点。如果存在(第59-66行),并且该节点未被标记,则添加操作返回false,表示键已经在集合中。然而,如果该节点尚未完全链接,则线程将等待,直到它完全链接(因为在节点完全链接之前,该键不在抽象集合中)。如果该节点被标记,则表示另一个线程正在删除该节点,因此执行添加操作的线程只需重试。
如果没有找到具有适当键的节点,则线程会锁定并验证findNode返回的所有前驱节点,直到达到新节点的高度(第69-84行)。该高度由add操作的开始处使用randomLevel函数确定。验证(第81-83行)检查对于每个层次i ≤ topNodeLayer,preds[i]和succs[i]是否在第i层仍然相邻,并且都没有被标记。如果验证失败,线程遇到了冲突的操作,因此释放它获取的锁(在第97行的finally块中)并重试。
如果线程成功锁定并验证findNode结果直到新节点的高度,则添加操作将保证成功,因为线程将持有所有锁,直到完全链接其新节点。在这种情况下,线程分配一个具有对应键和高度的新节点,将其链接到列表中,设置新节点的fullyLinked标志(这是添加操作的线性化点),然后在释放所有锁之后返回true(第86-97行)。写入newNode->nexts[i]的线程是唯一一种情况,其中线程修改了它没有锁定的节点的nexts字段。这是安全的,因为在线程将preds[i]->nexts[i]设置为newNode之后,newNode不会在第i层链接到列表中,而是在写入newNode->nexts[i]之后才链接。
bool add (int v){
int topLayer = randomLevel(MaxHeight);
Node∗ preds [MaxHeight] , succs[MaxHeight];
while(true){
int lFound = findNode(v, preds, succs);
if(lFound != −1){
Node∗ nodeFound = succs[lFound];
if(!nodeFound−>marked){
while (!nodeFound−>fullyLinked){;}
return false;
}
continue;
}
int highestLocked = −1;
try{
Node ∗pred, ∗succ, ∗prevPred = null;
bool valid = true;
for (int layer = 0; valid && (layer ≤ topLayer); layer++){
pred = preds[layer];
succ = succs[layer];
if(pred != prevPred) {
pred−>lock.lock();
highestLocked = layer;
prevPred = pred;
}
valid = !pred−>marked && !succ−>marked && pred−>nexts[layer] == succ;
}
if(!valid) continue;
Node∗ newNode = new Node (v, topLayer);
for(int layer = 0; layer ≤ topLayer; layer++){
newNode−>nexts[layer] = succs [layer];
preds[layer] −> nexts[layer] = newNode;
}
newNode −> fullyLinked = true;
return true;
} finally{
unlock(preds, highestLocked);
}
}
}
3.2 删除操作
删除操作(见图5)同样调用findNode函数来确定列表中是否存在具有适当键的节点。如果存在,则线程检查该节点是否“可以删除”(图6),这意味着它完全链接、未被标记,并且它是在其顶层找到的节点。如果节点满足这些要求,线程将锁定该节点并验证它是否仍未被标记。如果是这样,线程将标记该节点,逻辑上删除它(第111-121行);也就是说,节点的标记是删除操作的线性化点。
该过程的其余部分完成了“物理”删除操作,通过先锁定其所有层次上的前驱节点(直到删除节点的高度为止)(第124-138行),然后一次将节点从列表中剪接出来(第140-142行),从而将节点从列表中删除。为了维护跳跃表结构,节点在从更高层次拼接出来之前先从较低层次拼接出来(尽管为了确保没有死锁,如第4节所讨论的,锁的获取顺序是从较低层次向上获取)。与添加操作类似,在更改任何已删除节点的前驱节点之前,线程验证这些节点确实是已删除节点的前驱节点。这是通过weakValidate函数完成的,该函数与validate相同,只是当后继节点被标记时不会失败,因为在这种情况下,后继节点应该是刚刚被标记的待删除的节点。如果验证失败,则线程释放对旧前驱节点的锁定(但不包括已删除的节点),并尝试通过再次调用findNode来找到已删除节点的新前驱节点。然而,此时它已经设置了局部的isMarked标志,以便不会尝试标记另一个节点。在成功从列表中删除已删除节点后,线程释放所有锁,并返回true。
如果未找到节点,或者找到的节点不是“可以删除”的(即已被标记、未完全链接或未在其顶层找到),则操作简单地返回false(第148行)。容易看出,如果节点未被标记,这是正确的,因为对于任何键,跳跃表中最多只有一个具有该键的节点(即从左哨兵可达),并且一旦节点被放入列表中(必须通过findNode找到),它就不会被删除,直到被标记。然而,如果节点已被标记,该论证则变得更加棘手,因为在找到该节点时,它可能不在列表中,而列表中可能有具有相同键的某个未标记节点。然而,正如我们在第4节中所论证的那样,这种情况下,在执行删除操作期间必定存在某个时刻,该键不在抽象集合中。
bool remove (int v){
Node∗ nodeToDelete = null;
bool isMarked = false;
int topLayer = −1;
Node∗ preds[MaxHeight], succs[MaxHeight];
while(true){
int lFound = findNode(v, preds, succs);
if(isMarked || (lFound != −1 && okToDelete(succs[lFound],lFound))){
if(!isMarked){
nodeToDelete = succs[lFound];
topLayer = nodeToDelete −> topLayer;
nodeToDelete −> lock.lock();
if(nodeToDelete−>marked) {
nodeToDelete−>lock.unlock ();
return false;
}
nodeToDelete−>marked = true;
isMarked = true;
}
int highestLocked = −1;
try {
Node ∗pred, ∗succ, ∗prevPred = null;
bool valid = true;
for (int layer = 0; valid && (layer ≤ topLayer); layer++) {
pred = preds[layer];
succ = succs[layer];
if (pred != prevPred) {
pred−>lock.lock();
highestLocked = layer;
prevPred = pred;
}
valid = ! pred−>marked && pred−>nexts[layer] == succ;
}
if (!valid) continue;
for (int layer = topLayer; layer ≥ 0; layer−−) {
preds [layer]−>nexts [layer] = nodeToDelete−>nexts [layer];
}
nodeToDelete−>lock.unlock();
return true;
} finally {
unlock (preds, highestLocked);
}
}
else return false;
}
}
Figure 5: The remove method
bool okToDelete ( Node∗ candidate , int lFound ) {
return (candidate−>fullyLinked
&& candidate−>topLayer==lFound
&& !candidate−>marked);
}
Figure 6: The okToDelete method
bool contains (int v) {
Node∗ preds [MaxHeight] , succs[MaxHeight] ;
int lFound = findNode (v, preds, succs) ;
return ( lFound != −1
&& succs [lFound]−>fullyLinked
&& !succs [lFound]−>marked ) ;
}
Figure 7: The contains method
3.3 包含操作
最后,我们考虑包含操作(见图7),它只是调用findNode,并且当且仅当找到一个未标记、完全链接的具有适当键的节点时返回true。如果找到这样的节点,则根据定义可以立即得出结论,该键在抽象集合中。然而,如上所述,如果该节点已被标记,那么很难看出返回false是安全的。我们在第4节中对此进行了论证。
3.4 实现问题
我们使用Java编程语言实现了该算法,以便与Doug Lea在java.util.concurrent包中的非阻塞跳跃表实现进行比较。伪代码中的数组堆栈变量被线程本地变量所取代,我们使用了直接的锁实现(我们无法使用内置的对象锁,因为我们的获取和释放模式无法始终使用synchronized块来表示)。
所呈现的伪代码针对简单性而不是效率进行了优化,可以改进的方式有很多,我们在实现中应用了其中许多方式。例如,如果找到具有适当键的节点,则添加和包含操作无需继续查找;它们只需要确定该节点是否完全链接且未标记。如果是这样,包含操作可以返回true,添加操作可以返回false。如果不是,则包含操作可以返回false,添加操作要么在返回false之前等待(如果节点未完全链接),要么必须重试。然而,删除操作确实需要搜索到底层以找到要删除的节点的所有前驱节点,但是一旦找到并标记了某一层上的节点,它可以在较低层次上搜索确切的节点,而无需比较键。这是正确的,因为一旦线程标记了节点,其他线程就无法取消链接它。
此外,在伪代码中,findNode总是从可能的最高层开始搜索,尽管我们预期大部分时间最高层将是空的(即只有两个哨兵节点)。通过维护一个跟踪最高非空层的变量,很容易因为每当该变量发生变化时,导致变化的线程必须锁定左哨兵。与非阻塞版本相比,这种容易性存在差异,因为并发的删除和添加操作之间的竞争可能导致记录的跳跃表高度小于其最高节点的实际高度。
4 正确性
在本节中,我们概述我们的跳跃表算法的证明。我们要展示四个属性:算法实现了可线性化的集合、它是无死锁的、contains操作是无等待的,以及底层数据结构维护了一个正确的跳跃表结构,我们将在下面更详细地定义。
4.1 可线性化性
在证明过程中,我们对初始化做出了以下简化假设:节点被初始化为具有其键和高度,它们的nexts数组被初始化为全部为null,它们的fullyLinked和marked字段被初始化为false。此外,为了推理的目的,我们假设节点永远不会被回收,并且有无穷无尽的新节点可用(否则,我们需要修改算法以处理节点耗尽的情况)。
我们首先得出以下观察结果:节点的键永远不会更改(即key = k是稳定的),节点的marked和fullyLinked字段永远不会被设置为false(即marked和fullyLinked是稳定的)。虽然初始时nexts[i]为null,但它永远不会被写入null(即nexts[i] 6= null是稳定的)。此外,线程只有在持有节点的锁时才会写入节点的marked或nexts字段(唯一的例外是在链接节点到第i层之前的add操作中写入节点的nexts[i])。
根据这些观察结果和对代码的检查,我们可以很容易地看出,在任何操作中,在调用findNode后,对于所有的i,我们有preds[i]->key < v和succs[i]->key ≥ v,并且对于i > lFound(即findNode返回的值),有succs[i]->key > v。此外,在remove操作中,只有在该节点被其他线程标记之前,nodeToDelete才会被设置一次,并且此线程在完成操作之前,线程的isMarked变量将始终为true。我们还通过okToDelete知道节点是完全链接的(实际上只有完全链接的节点才能被标记)。
此外,验证和在写入节点之前锁定节点的要求确保在成功验证后,验证检查的属性(对于add和remove而言略有不同)在释放锁之前保持为true。
我们可以利用这些属性得出以下基本引理(fundamental lemma):
Lemma 1 For a node n and 0 ≤ i ≤ n->topLayer:
n->nexts[i] 6= null =⇒ n->key < n->nexts[i]->key
我们定义关系→i,表示在第i层上,如果m->nexts[i] = n或者存在m0使得m →i m0且m0->nexts[i] = n,则表示m导向n(读作“m leads to n at layer i”)。因为一个节点在任何层上最多只有一个直接后继节点,所以→i关系在第i层上“遵循”一个链表的结构,特别地,跳表中的第i层列表包括那些满足LSentinel →i n(以及LSentinel本身)的节点n。另外,根据引理1,如果m →i n且m →i n0且n->key < n0->key,则n →i n0。
基于这些观察,我们可以证明,在算法的任何可达状态下,如果m →i n,则在任何后续状态中,除非存在将n从第i层列表中切割的操作(即执行第141行),否则m →i n将继续成立。这个结论在最近的一篇论文中正式证明了懒惰列表算法,并且该证明可以适应这个算法。因为在n被切割出列表之前,它必须已经被标记,而且由于fullyLinked标志在初始化后不会被设置为false,这个结论意味着只有通过标记节点才能从抽象集合中移除键,而我们之前已经证明标记节点是成功删除操作的线性化点。
类似地,我们可以观察到,如果LSentinel →i n在算法的某个可达状态中不成立,则除非在某个执行中出现n = newNode的情况(如前所述,前一行不会改变第i层的列表,因为newNode尚未链接)。然而,该行的执行发生在newNode被插入但尚未完全链接的过程中。因此,将节点添加到任何级别的列表的唯一操作是设置节点的fullyLinked标志。
最后,我们论证如果一个线程找到了一个标记节点,那么该节点的键在该线程执行操作的过程中必定不在列表中。有两种情况:如果节点在线程调用操作时已经被标记,则该节点必须在那个时刻已经存在于跳表中,因为标记节点不能添加到跳表中(只能将新分配的节点添加到跳表中),并且由于跳表中没有两个具有相同键的节点,因此跳表中没有未标记的节点具有该键。因此,在调用操作时,键不在跳表中。另一种情况是,如果线程调用操作时节点没有被标记,那么它必须在第一个线程发现它之前被其他线程标记,然后,根据我们之前的论证,当其他线程首次标记节点时,键在该线程的操作执行期间不在抽象集合中。这个结论在简单懒惰列表[1]的形式证明中也得到了证实,而且可以适用于这个算法。
综上所述,我们通过观察和代码分析,证明了一些重要的性质。在任何操作中,在调用findNode之后,我们有preds[i]->key < v且succs[i]->key ≥ v对于所有i成立,并且对于i > lFound(findNode返回的值),succs[i]->key > v。对于remove操作中的线程,nodeToDelete只被设置一次,除非该节点被其他线程标记,该线程将标记该节点,并且在完成操作之前,线程的isMarked变量将保持为true。我们还通过okToDelete知道该节点是完全链接的(实际上,只有完全链接的节点才能被标记)。
此外,验证和在写入节点之前要求锁定节点的要求确保在成功验证之后,验证所检查的属性(对于add和remove来说略有不同)在释放锁之前保持不变。
基于这些性质,我们可以得出以下基本引理的证明。
4.2 维护跳跃表的不变性
我们的算法保证跳跃表的不变性在任何时候都得到保持。通过“跳跃表的不变性”,我们指的是每个层次的列表是低层次列表的子列表。保持这种结构的重要性在于,跳跃表的复杂度分析要求具备这种结构。 要看到算法如何保持跳跃表的结构,注意到将新节点链接到跳跃表的过程始终从底层到顶层进行,并且在插入节点时持有所有即将成为该节点前驱节点的锁。另一方面,当从列表中删除节点时,高层节点先于低层节点被取消链接,同样在删除节点的直接前驱节点上持有锁定。
保持跳跃表结构的性质,在锁无关的算法中并不保证。在该算法中,在将节点链接到底层后,将节点从顶层到底层在其余的层次上链接。这可能导致节点仅在其顶层和底层上链接,使得顶层的列表不是其下一层列表的子列表,例如。此外,在除底层之外的任何层次上尝试链接节点时,不会进行重试,因此这种不符合跳跃表结构的状态可能会无限期地持续存在。
这是我们基于锁的算法与锁无关算法之间的一个重要区别。我们的基于锁的算法通过明确获取锁并在从底层到顶层链接节点时维护必要的锁定纪律,以确保在任何时候都保持跳跃表的结构。
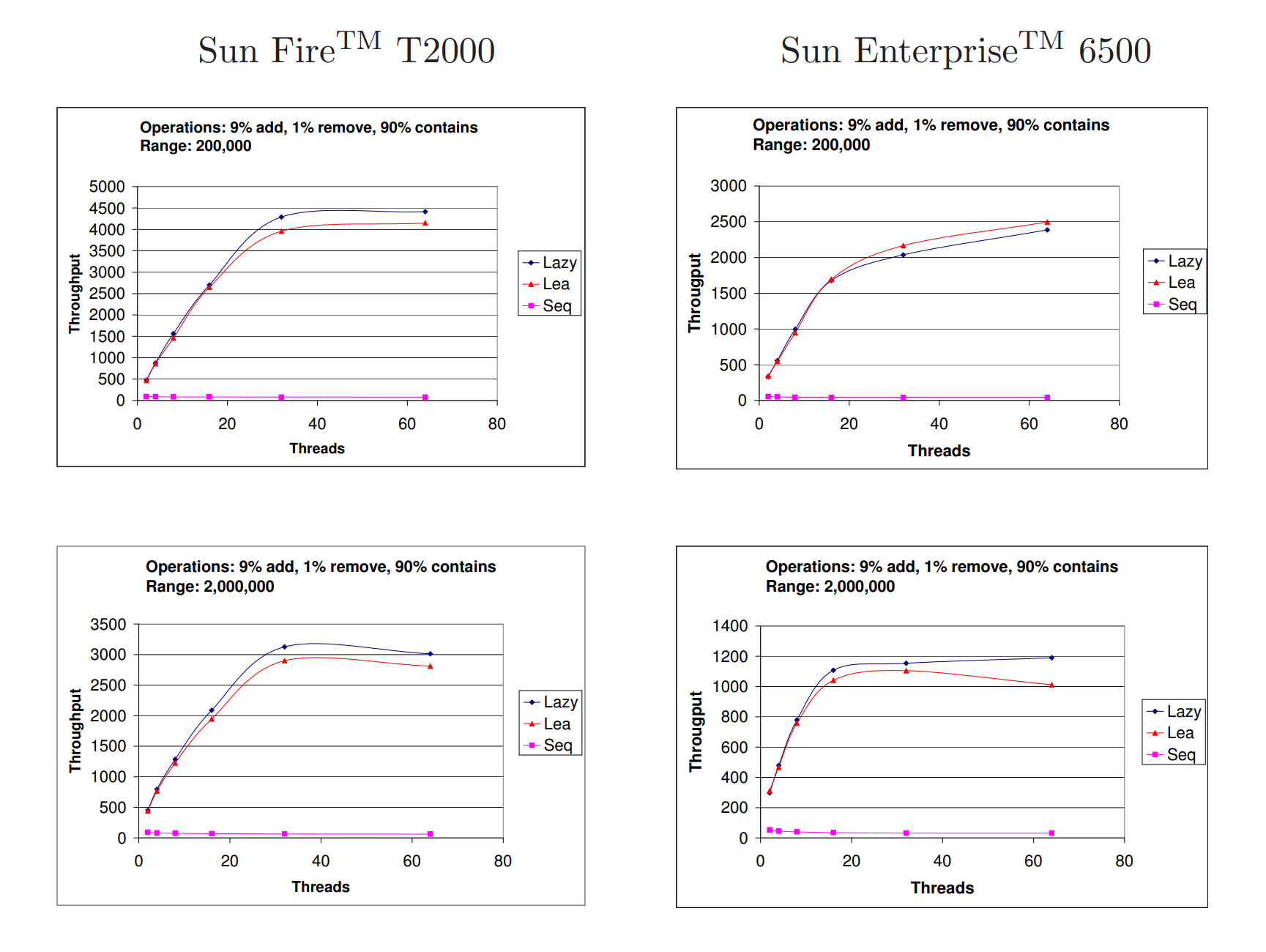
Figure 8: 在执行1,000,000次操作的情况下,每毫秒的吞吐量,其中有9%的添加操作,1%的删除操作和90%的包含操作,键范围分别为200,000和2,000,000。
4.3 死锁自由和无等待性
该算法是死锁自由的,因为线程总是先获取具有较大键的节点上的锁。更具体地说,如果一个线程持有具有键v的节点上的锁,则它不会尝试获取具有大于或等于v的键的节点上的锁。我们可以看到这是正确的,因为添加和删除方法都从底层向上获取前驱节点的锁,并且前驱节点的键小于较低层的其他前驱节点的键。唯一的其他锁获取是删除操作删除的节点。这是该操作获取的第一个锁,它的键大于任何前驱节点的键。
包含操作是无等待的也很容易理解:它不获取任何锁,也不会进行重试;它只搜索一次列表。
5 性能
我们通过在Java编程语言中实现我们的跳跃表算法来评估其性能,正如之前所描述的那样。我们将我们的实现与Doug Lea在java.util.concurrent包的ConcurrentSkipListMap类中的非阻塞跳跃表实现进行了比较。据我们所知,这是目前最好的广泛可用的并发跳跃表实现。我们还实现了一个简单的顺序跳跃表,其中的方法通过同步来确保线程安全,作为实验中的基准。本节中,我们描述了从这些实验中获得的一些结果。
我们使用两个具有不同架构的多处理器系统进行实验。第一个系统是基于单个UltraSPARC°r T1处理器的Sun Fire T2000服务器,该处理器包含8个计算核心,每个核心具有4个硬件线程,主频为1200 MHz。每个具有4个线程的核心具有一个8KB级1数据缓存和一个16KB指令缓存。所有8个核心共享一个3MB级2统一(指令和数据)缓存和一个4路交错的32GB主存储器。数据访问延迟比大约为1:8:50(L1:L2:内存访问)。另一个系统是较旧的Sun Enterprise 6500服务器,它包含15个系统板,每个板上有两个主频为400 MHz的UltraSPARC°r II处理器和2GB内存,总共有30个处理器和60GB内存。每个处理器在芯片上有一个16KB的数据级1缓存和一个16KB的指令缓存,以及一个8MB的外部缓存。系统时钟频率为80 MHz。
我们展示了从一个空的跳跃表开始,每个线程执行一百万(1,000,000)个随机选择的操作的实验结果。我们变化了线程数量,添加、删除和包含操作的相对比例,以及选择键的范围。每个操作的键是从指定范围均匀随机选择的。 在接下来的图表中,我们比较每毫秒操作的吞吐量,所显示的结果是每组参数的六次运行的平均值。
图8展示了实验结果,其中9%的操作是添加操作,1%的操作是删除操作,剩下的90%是包含操作,键的范围为20万或200万。不同的范围会产生不同程度的竞争,其中200,000范围的竞争更高,与2,000,000范围相比。从这些实验中可以看出,我们的实现和Lea的实现都具有良好的可扩展性(而顺序算法如预期的那样相对平坦)。除了在旧系统上使用200,000范围的情况下,我们的实现在所有情况下都稍微占优势。
图9展示了一系列实验的结果,其中添加操作的百分比变化,而删除操作的百分比固定为1%,剩余的百分比分配给包含操作。键的范围设置为两百万。如图所示,我们的实现在不同的添加操作百分比下优于Lea的实现,展示了它的可伸缩性和效率。
总体而言,实验结果表明,我们基于锁的并发跳表算法的性能与最佳的无锁实现相当,甚至更好。它在常见的使用模式下实现了高度的可伸缩性和效率,其中搜索操作占主导地位,插入操作占主导地位。我们的算法始终保持跳表的特性,简化了对正确性的推理,并且它是无死锁和无等待的,确保所有线程都能取得进展。
这些性能结果验证了我们基于锁的并发跳表算法的有效性,并突显了它作为现有并发跳表实现的可行替代方案的潜力,特别是在强调简单性、可伸缩性和性能的应用中。
在下一组实验中,我们运行了更高比例的添加和删除操作,分别为20%和10%(剩余70%的包含操作)。结果如图9所示。可以看到,在T2000系统上,两种实现的性能相似,Lea在多程序环境下,当范围较小(更高的竞争)时略有优势。而在范围较大时情况则相反。这种现象在旧系统上更为明显:在范围较小、64个线程的情况下,Lea的实现优势达到13%,而在范围较大、相同数量的线程下,我们的算法有20%的优势。
为了探究这种现象,我们进行了一项具有显著较高竞争水平的实验:半数添加操作和半数删除操作,范围为20万。结果如图10所示。可以清楚地看到,在这种竞争水平下,我们的实现的吞吐量在接近多程序区域时迅速下降,特别是在T2000系统上。这种下降并不令人意外:在我们当前的实现中,当添加或删除操作无法通过验证或无法立即获取锁时,它只是调用yield;没有适当的机制来管理竞争。由于添加和删除操作要求在锁定之前搜索阶段看到的前驱节点不发生更改,我们预计在高竞争下,它们将反复失败。因此,我们预计引入退避机制或其他形式的竞争控制将极大地提高性能。为了验证高冲突水平确实是问题所在,我们添加了计数器来计算实验期间每个线程执行的重试次数。计数器确实显示,在64个线程运行时执行了许多次重试,特别是在T2000系统上。大多数重试是由添加方法执行的,这是有道理的,因为删除方法在搜索更低层的前驱节点之前标记要删除的节点,这可以防止并发添加操作更改这些前驱节点的next指针。
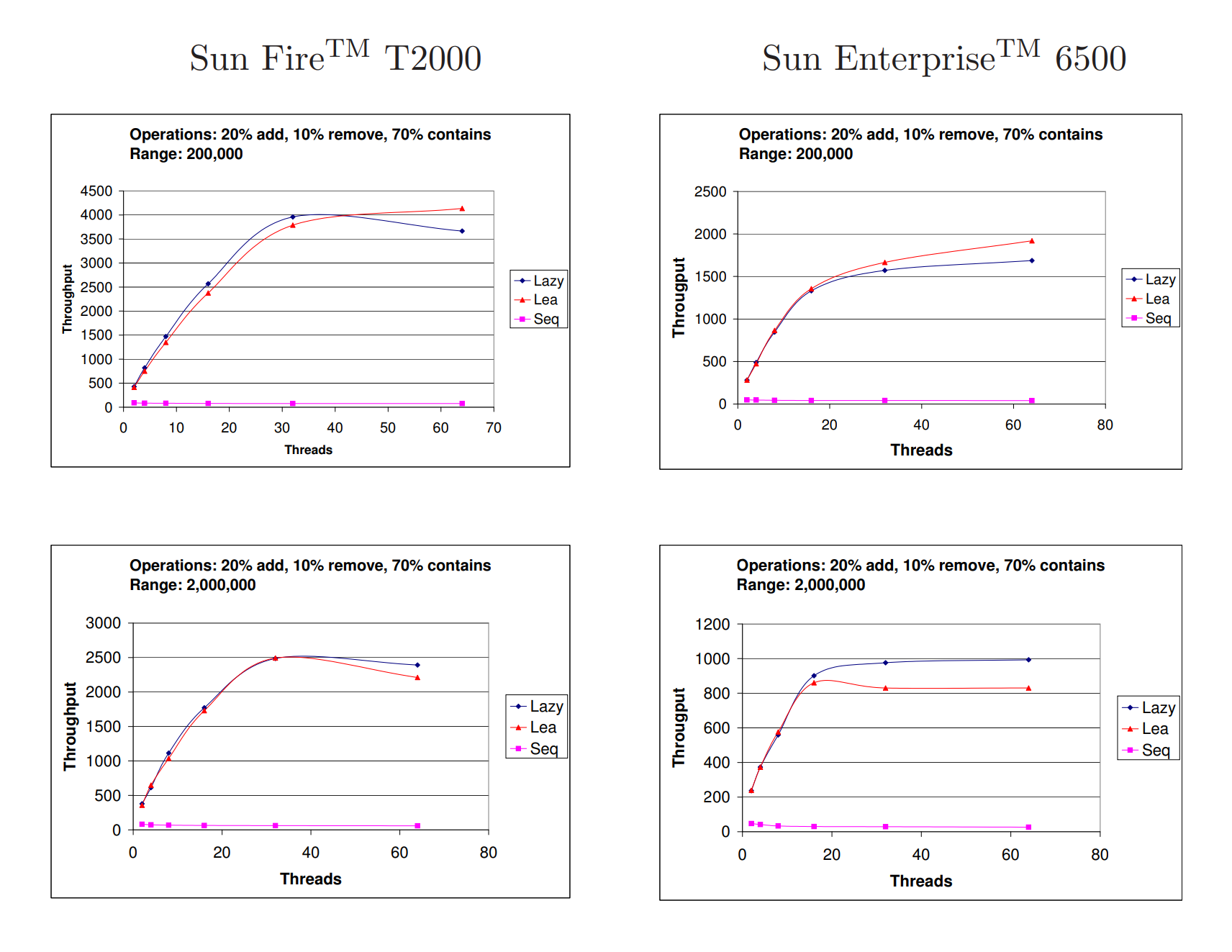
Figure 9: 在执行1,000,000次操作的情况下,每毫秒的吞吐量,其中有20%的添加操作,10%的删除操作和70%的包含操作,键范围分别为200,000和2,000,000。
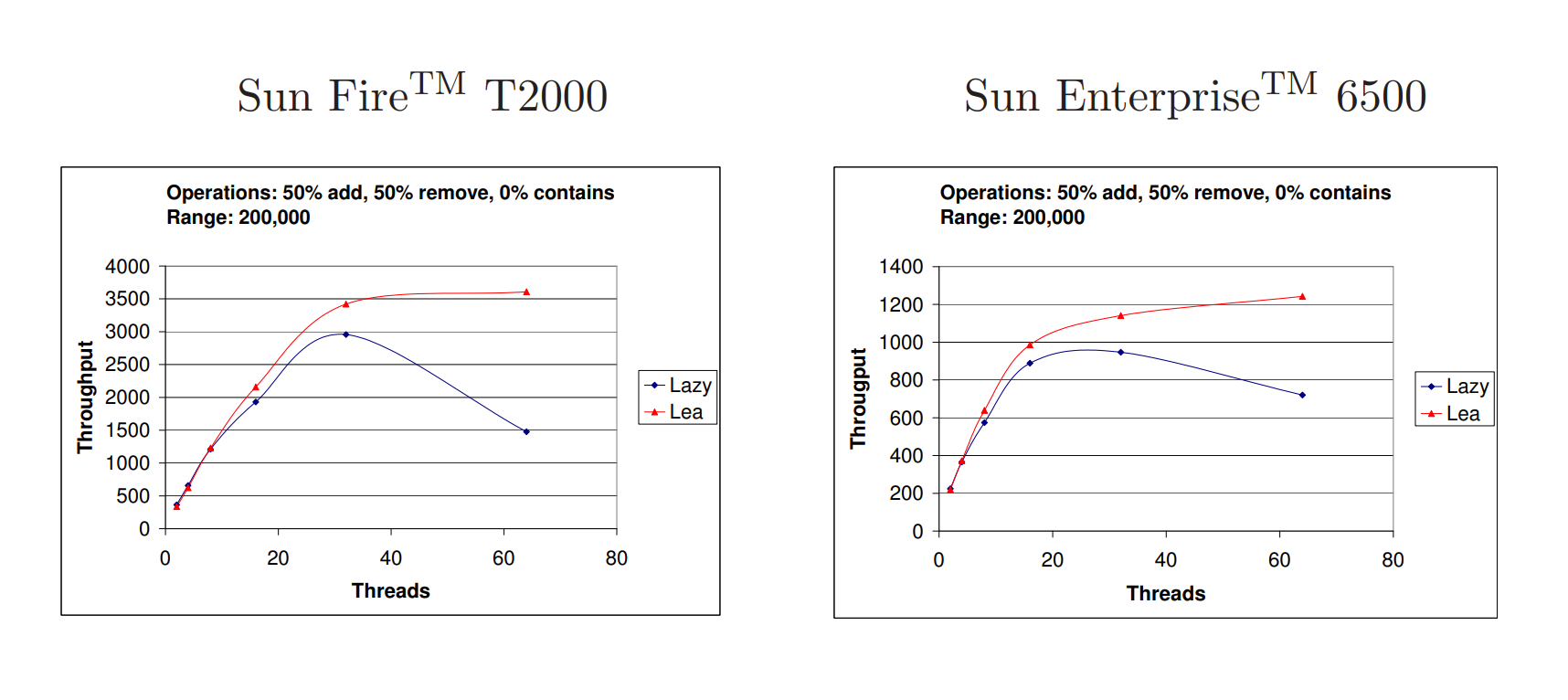
Figure 10: 在执行1,000,000次操作的情况下,每毫秒的吞吐量,其中有50%的添加操作和50%的删除操作,键范围为200,000。
6 结论
我们展示了如何使用一种非常简单的算法构建可扩展的高并发跳表。我们的实现还不完善,显然在处理高度竞争的情况下可以从更好的竞争控制机制中获益。尽管如此,我们相信即使在其原始形式下,对于大多数使用情况来说,它仍然是一种有趣且可行的替代方案,可以替代ConcurrentSkipListMap。
引用
[1] Colvin, R., Groves, L., Luchangco, V., and Moir, M. Formal verification of a lazy concurrent list-based set. In Proceedings of Computer-Aided Verification (Aug. 2006).
[2] Fraser, K. Practical Lock-Freedom. PhD thesis, University of Cambridge, 2004.11
[3] Fraser, K., and Harris, T. Concurrent programming without locks. Unpublished manuscript, 2004.
[4] Heller, S., Herlihy, M., Luchangco, V., Moir, M., Shavit, N., and Scherer III, W. N. A lazy concurrent list-based set algorithm. In Proceedings of 9th International Conference on Principles of Distributed Systems (Dec. 2005).
[5] Herlihy, M., Luchangco, V., and Moir, M. The repeat offender problem: A mechanism for supporting dynamic-sized, lock-free data structures. In Proceedings of Distributed Computing: 16th International Conference (2002). [6] Herlihy, M., and Wing, J. Linearizability: A correctness condition for concurrent objects. ACM Transactions on Programming Languages and Systems 12, 3 (July 1990), 463–492.
[7] Lea, D. Personal communication, 2005.
[8] Lea, D. ConcurrentSkipListMap. In java.util.concurrent.
[9] Michael, M. Hazard pointers: Safe memory reclamation for lock-free objects. IEEE Transactions on Parallel and Distributed Systems 15, 6 (June 2004), 491–504.
[10] Pugh, W. Concurrent maintenance of skip lists. Tech. Rep. CS-TR-2222, 1990.
[11] Pugh, W. Skip lists: A probabilistic alternative to balanced trees. Communications of the ACM 33, 6 (June 1990), 668–676
论文实现
原本我是打算按照此篇论文自行实现一个并发安全跳表的,但是我在github上找到了一个基于此论文的优秀的golang开源实现,代码的质量很高,在此篇博客中,我将基于这个开源代码进行论文实现的代码分析。
原仓库:
https://github.com/zhangyunhao116/skipmap
源作者的代码使用了Golang的泛型,但由于在本篇文章中基于泛型实现来分析源码会导致理解成本的增加,因此我在原作者的代码上进行了部分修改,以降低额外的学习难度。
先来看一下我们最后要怎么使用这个跳表,从一个使用案例作为代码分析的入口
func TestSKL(t *testing.T) {
// 构建跳表
skl := NewSkipList()
// 构建测试用的K、V
k := &Item{Key: []byte("key")}
// 测试 key2 为 nil
k2 := &Item{Key: nil}
v1 := "val"
v2 := "val2"
v3 := "val3"
// 加入 k v1
skl.Store(k, v1)
checkLoad(skl.Load(k))
// 删除 k
skl.Delete(k)
checkLoad(skl.Load(k))
// 加入 k v2
skl.Store(k, v2)
checkLoad(skl.Load(k))
// 加入 k v1
skl.Store(k, v1)
checkLoad(skl.Load(k))
// 不加入 k2 的时候,能否查找到 nil
checkLoad(skl.Load(k2))
skl.Store(k2, v3)
checkLoad(skl.Load(k2))
}
type Item struct {
Key []byte
}
func (i *Item) Less(key ComparableKey) bool {
return bytes.Compare(i.Key, key.(*Item).Key) == -1
}
func checkLoad(v any, ok bool) {
if ok {
fmt.Println(v.(string))
} else {
fmt.Println("not found key")
}
}
NewSkipList()
先来看一下核心的结构体
// ConcurrentSkipList 跳表的顶层结构
type ConcurrentSkipList struct {
length int64
highestLevel uint64 // highest level for now
header *Node
}
ConcurrentSkipList是这个跳表的顶层结构体,拥有三个字段,维护着跳表的一些元信息,包括长度和最大高度,然后维护着头节点的引用
// 跳表的节点
type Node struct {
key ComparableKey
value unsafe.Pointer // *any
flags bitflag
next tower // [level]*orderednode
mu sync.Mutex
level uint32
}
Node是跳表最核心的节点,是跳表最基小单元。
每个Node中维护着当前节点的Key、Value,节点状态标记(flags)、指向下一个节点的指针列表(tower)、必要的锁、当前节点的高度的信息
其中Key的类型是 ComparbleKey,是一个接口,需要在用户的调用方自行实现
type ComparableKey interface {
Less(than ComparableKey) bool
}
bitflag结构体本质上就是两个bool值,用来标记是否已经属于全连接状态(前置节点和后继节点的指针全部已经准备好,此时这个节点已经可以被查询、删除、修改了)和处于删除标记状态,主要包含了set和get方法用来读取和修改标记位
const (
fullyLinked = 1 << iota
deletedMarked
)
// concurrent-safe bitflag.
type bitflag struct {
data uint32
}
func (f *bitflag) SetTrue(flags uint32) {
for {
old := atomic.LoadUint32(&f.data)
if old&flags != flags {
// Flag is 0, need set it to 1.
n := old | flags
if atomic.CompareAndSwapUint32(&f.data, old, n) {
return
}
continue
}
return
}
}
func (f *bitflag) SetFalse(flags uint32) {
for {
old := atomic.LoadUint32(&f.data)
check := old & flags
if check != 0 {
// Flag is 1, need set it to 0.
n := old ^ check
if atomic.CompareAndSwapUint32(&f.data, old, n) {
return
}
continue
}
return
}
}
func (f *bitflag) Get(flag uint32) bool {
return (atomic.LoadUint32(&f.data) & flag) != 0
}
func (f *bitflag) MGet(check, expect uint32) bool {
return (atomic.LoadUint32(&f.data) & check) == expect
}
tower是当前节点的指向下一个节点的指针列表,因为在跳表的示意图中,一个跳表有很多个后继指针,摞起来像个塔一样,所以是不是用tower来表示非常形象hhh,在tower中主要也就是get和set方法,用来读取修改节点在某层的后继指针
type tower [maxLevel]*Node
func (t *tower) load(i int) *Node {
return t[i]
}
func (t *tower) store(i int, node *Node) {
t[i] = node
}
// 这里看上去有些负载,因为atomic.LoadPointer方法接收的是*unsafe.Pointer参数,
// 而unsafe.Pointer(&t[i]))只能转换到unsafe.Pointer类型,而且不能直接取地址
// 所以还要通过(*unsafe.Pointer)来转化类型,才能将数据转成atomic.LoadPointer能接收的类型
func (t *tower) atomicLoad(i int) *Node {
return (*Node)(atomic.LoadPointer((*unsafe.Pointer)(unsafe.Pointer(&t[i]))))
}
// 和上面类似
func (t *tower) atomicStore(i int, node *Node) {
atomic.StorePointer((*unsafe.Pointer)(unsafe.Pointer(&t[i])), unsafe.Pointer(node))
}
NewSkipList()方法
从函数名上就可以得知,这个函数的作用是新建一个跳表的实例,在内部实现中,创建了跳表的第一个节点,并且给节点设置为全连接的状态,创建跳表实例并返回这个实例给调用方
func NewSkipList() *ConcurrentSkipList {
// 创建第一个节点
h := newNode(nil, nil, maxLevel)
// 设置为全连接状态
h.flags.SetTrue(fullyLinked)
return &ConcurrentSkipList{
header: h,
}
}
newNode方法
传入key、value、level,构建一个Node并返回
func newNode(key ComparableKey, value any, level int) *Node {
node := &Node{
key: key,
level: uint32(level),
}
node.storeVal(value)
return node
}
一些Node的基本操作方法,包括对值的get/set和对后继节点的get/set还包含了原子操作
func (n *Node) storeVal(value any) {
atomic.StorePointer(&n.value, unsafe.Pointer(&value))
}
func (n *Node) loadVal() any {
return *(*any)(atomic.LoadPointer(&n.value))
}
func (n *Node) loadNext(i int) *Node {
return n.next.load(i)
}
func (n *Node) storeNext(i int, node *Node) {
n.next.store(i, node)
}
func (n *Node) atomicLoadNext(i int) *Node {
return n.next.atomicLoad(i)
}
func (n *Node) atomicStoreNext(i int, node *Node) {
n.next.atomicStore(i, node)
}
findNode(…)
查找某一个节点,如果找到立即返回,未找到则返回nil,这是一个内部使用的辅助方法。
// findNode takes a key and two maximal-height arrays then searches exactly as in a sequential skipmap.
// The returned preNodes and nextNodes always satisfy preNodes[i] > key >= nextNodes[i].
// (without fullpath, if find the node will return immediately)
func (s *ConcurrentSkipList) findNode(key ComparableKey, preNodes *[maxLevel]*Node, nextNodes *[maxLevel]*Node) *Node {
x := s.header
// 从高最高节点开始查询
for i := int(atomic.LoadUint64(&s.highestLevel)) - 1; i >= 0; i-- {
// 原子获取最高层的下一个节点
nextNode := x.atomicLoadNext(i)
// 循环,直到找到目标节点的后继点击(或者尾节点)
for nextNode != nil && (nextNode.key.Less(key)) {
// 如果下一个节点的键值小于目标键值,说明还需要继续向后遍历,更新当前节点为下一个节点,
// 并更新下一个节点为当前节点的下一个节点。这个过程会在当前层级上持续进行,
// 直到找到一个下一个节点的键值大于等于目标键值,或者下一个节点为nil。
x = nextNode
nextNode = x.atomicLoadNext(i)
}
// 此时next node
// 在每个层级上,代码都会记录当前节点作为前驱节点,并记录下一个节点作为后继节点,存储在preNodes和nextNodes数组中。
// 这样,当查找结束时,preNodes和nextNodes数组中存储的节点序列就构成了一个部分有序的路径,满足preNodes[i] > key >= nextNodes[i]的条件。
preNodes[i] = x
nextNodes[i] = nextNode
// Check if the key already in the skipmap.
if nextNode != nil && nextNode.key == key {
// 如果在查找过程中找到一个节点的键值与目标键值相等,说明目标键值已经存在于跳表中,直接返回该节点
return nextNode
}
}
// 如果没有找到,返回nil
return nil
}
用于delete的find辅助方法
// findNodeDelete takes a key and two maximal-height arrays then searches exactly as in a sequential skip-list.
// The returned preNodes and nextNodes always satisfy preNodes[i] > key >= nextNodes[i].
func (s *ConcurrentSkipList) findNodeDelete(key ComparableKey, preNodes *[maxLevel]*Node, nextNodes *[maxLevel]*Node) int {
// lFound represents the index of the first layer at which it found a node.
lFound, x := -1, s.header
// 代码通过循环遍历每个层级的链表,从最高层级开始向下搜索,找到满足条件的节点。
for i := int(atomic.LoadUint64(&s.highestLevel)) - 1; i >= 0; i-- {
nextNode := x.atomicLoadNext(i)
// 在每个层级上,代码比较节点的键与目标键的大小关系,根据节点的键是否小于目标键决定向后移动到下一个节点。
for nextNode != nil && (nextNode.key.Less(key)) {
x = nextNode
nextNode = x.atomicLoadNext(i)
}
// 同时,代码记录节点的前驱节点和后继节点到预定义的数组中。
preNodes[i] = x
nextNodes[i] = nextNode
// Check if the key already in the skip list.
if lFound == -1 && nextNode != nil && nextNode.key == key {
// 如果在搜索过程中找到了目标节点(即节点的键等于目标键),则记录该节点所在的层级索引为lFound,表示找到了节点。
lFound = i
}
}
// 最后,代码返回lFound,即找到的节点所在的最高层级索引。
return lFound
}
可以看到,findNode和findNodeDelete都是实际查找节点的辅助方法,使用的时候会传入目标节点的前置指针列表和后继指针列表的引用,在方法执行过程中对其赋值,在查找过程中都是从最高层向下逐级查找,在返回值上面,findNode会返回找到的节点的引用,而findNodeDelete会返回能找到此节点的最高层级,这部分的差异在下文会有所解释
Load(key)
供外层调用的核心方法,用于加载一个Key所对应的Value
// Load returns the value stored in the map for a key, or nil if no
// value is present.
// The ok result indicates whether value was found in the map.
func (s *ConcurrentSkipList) Load(key ComparableKey) (value any, ok bool) {
// 从头节点开始
x := s.header
// 从最高节点开始
for i := int(atomic.LoadUint64(&s.highestLevel)) - 1; i >= 0; i-- {
nex := x.atomicLoadNext(i)
for nex != nil && (nex.key.Less(key)) {
x = nex
nex = x.atomicLoadNext(i)
}
// Check if the key already in the skip list.
// 如果找到了数据
if nex != nil && nex.key == key {
// 检查数据是否是就绪状态(处于全链接状态)
if nex.flags.Get(fullyLinked) {
// 如果就绪,直接返回
return nex.loadVal(), true
}
return
}
}
return
}
可以看到,这Load方法是完全不加锁的,而是在返回数据时进行一个原子操作,如果节点处于就绪状态,直接返回,如果处于未就绪状态,我们可以认为在逻辑上,这个节点在这个时间点上是不在这个跳表中的,直接返回空
Store(key, value)
供外层调用的核心方法,用于存储一对Key-Value
// Store sets the value for a key.
func (s *ConcurrentSkipList) Store(key ComparableKey, value any) {
// 获取一个随机的高度
level := s.randomlevel()
// 初始化目标节点的前置、后继节点的指针列表
var preNodes, nextNodes [maxLevel]*Node
for {
nodeFound := s.findNode(key, &preNodes, &nextNodes)
// 代码首先调用findNode函数查找指定键的节点。如果找到了节点,则表示目标键已经存在于跳表中。
if nodeFound != nil { // indicating the key is already in the skip-list
if !nodeFound.flags.Get(deletedMarked) {
// We don't need to care about whether or not the node is fully linked,
// just replace the value.
// 代码检查该节点是否被标记(deletedMarked),如果没有被标记,则说明该节点是完全链接的,直接替换其值即可。
nodeFound.storeVal(value)
return
}
// If the node is deletedMarked, represents some other goroutines is in the process of deleting this node,
// we need to add this node in next loop.
// 如果节点被标记了,表示其他协程正在删除该节点的过程中,需要继续下一轮循环。
continue
}
// 如果没有找到节点,则表示目标键不存在于跳表中,需要将其添加到跳表中。
// Add this node into skip list.
var (
highestLocked = -1 // the highest level being locked by this process
valid = true
preNode, nextNode, prevPred *Node
)
for layer := 0; valid && layer < level; layer++ {
// 代码进入一个循环,在每次循环中尝试添加节点到不同的层级。
// 在循环内部,代码对前驱节点和后继节点进行加锁,并进行一系列有效性检查。
preNode = preNodes[layer] // target node's previous node
nextNode = nextNodes[layer] // target node's next node
if preNode != prevPred { // the node in this layer could be locked by previous loop
preNode.mu.Lock()
highestLocked = layer
prevPred = preNode
}
// valid check if there is another node has inserted into the skip list in this layer during this process.
// It is valid if:
// 1. The previous node and next node both are not deletedMarked.
// 2. The previous node's next node is nextNode in this layer.
// 在有效性检查中,代码检查前驱节点和后继节点是否被标记,并且前驱节点的下一个节点是否为后继节点。
// 这些检查用于确保在添加节点过程中没有其他协程插入节点。
valid = !preNode.flags.Get(deletedMarked) && (nextNode == nil || !nextNode.flags.Get(deletedMarked)) && preNode.loadNext(layer) == nextNode
}
if !valid {
// 如果检查失败,说明在此过程中有其他节点插入了跳表,代码需要释放已加的锁,并继续下一轮循环。
unlockordered(preNodes, highestLocked)
continue
}
// 如果有效性检查通过,代码创建一个新的节点(nn),设置其键值和层级,并将其链接到各个层级的前驱节点和后继节点之间。
nn := newNode(key, value, level)
for layer := 0; layer < level; layer++ {
nn.storeNext(layer, nextNodes[layer])
preNodes[layer].atomicStoreNext(layer, nn)
}
// 最后,将新节点标记为完全链接(fullyLinked),释放之前加的锁,并增加跳表的长度计数。
nn.flags.SetTrue(fullyLinked)
unlockordered(preNodes, highestLocked)
atomic.AddInt64(&s.length, 1)
return
}
}
func unlockordered(preNodes [maxLevel]*Node, highestLevel int) {
var prevPred *Node
// 从高层向低层逐一解锁
for i := highestLevel; i >= 0; i-- {
if preNodes[i] != prevPred { // the node could be unlocked by previous loop
preNodes[i].mu.Unlock()
prevPred = preNodes[i]
}
}
}
总的来说,Store操作就是先通过findNode找节点,如果存在,直接通过原子操作修改值就OK,如果不存在,则给待加入节点的前驱后继节点自底向上逐层加锁,加锁成功后再次检查安全性,查看是否在加锁过程总有其它加入的节点,在通过检测后进行添加节点,逐层修改前驱节点的指向,最后将该新节点设置为全链接状态,逐层释放锁,增加跳表长度信息,添加完成。
多数的逻辑都很清晰,主要难理解的地方在于那个校验的过程,我们来梳理一下
valid = !preNode.flags.Get(deletedMarked) && (nextNode == nil || !nextNode.flags.Get(deletedMarked)) && preNode.loadNext(layer) == nextNode
!preNode.flags.Get(deletedMarked): 检查前驱节点preNode的flags属性是否包含deletedMarked标记,即确认前驱节点没有处在删除过程中。nextNode == nil || !nextNode.flags.Get(deletedMarked): 待插入节点的后继节点是否为空或者没有在删除过程中,即确认后继节点的指针是可以指向的。preNode.loadNext(layer) == nextNode: 确认前驱节点在当前层的后继节点为待插入节点的后继节点。
当以上三点全部通过的时候,则正面前后的节点都是安全的,所以可以执行插入操作
// 生成随机高度,并在必要的时候更新最高高度
// randomlevel returns a random level and update the highest level if needed.
func (s *ConcurrentSkipList) randomlevel() int {
// Generate random level.
// 可以直接使用抛硬币的方式生成节点高度
level := randomLevel()
// Update highest level if possible.
for {
hl := atomic.LoadUint64(&s.highestLevel)
if uint64(level) <= hl {
break
}
if atomic.CompareAndSwapUint64(&s.highestLevel, hl, uint64(level)) {
break
}
}
return level
}
Delete(key)
供外层调用的核心方法,用于删除一对Key-Value
// Delete deletes the value for a key.
func (s *ConcurrentSkipList) Delete(key ComparableKey) bool {
var (
nodeToDelete *Node
isMarked bool // represents if this operation mark the node
topLayer = -1
preNodes, nextNodes [maxLevel]*Node
)
for {
// 代码首先调用findNodeDelete函数查找指定键的节点,并检查是否可以进行删除操作。如果满足以下条件之一,则可以进行删除操作:
lFound := s.findNodeDelete(key, &preNodes, &nextNodes)
// 如果前一次循环已经标记了要删除的节点(isMarked为true)。
if isMarked || // this process mark this node or we can find this node in the skip list
// 如果找到了目标节点,并且该节点(待删除的节点)被完全链接(fullyLinked),且该节点在当前层级的最高层级。
lFound != -1 && nextNodes[lFound].flags.Get(fullyLinked) && (int(nextNodes[lFound].level)-1) == lFound {
if !isMarked { // we don't mark this node for now
nodeToDelete = nextNodes[lFound]
topLayer = lFound
nodeToDelete.mu.Lock()
if nodeToDelete.flags.Get(deletedMarked) {
// The node is deletedMarked by another process,
// the physical deletion will be accomplished by another process.
// 如果上述条件不满足,则返回false,表示删除操作无法执行,当前节点被其它线程删除中。
nodeToDelete.mu.Unlock()
return false
}
// 添加删除标记
nodeToDelete.flags.SetTrue(deletedMarked)
isMarked = true
}
// Accomplish the physical deletion.
var (
highestLocked = -1 // the highest level being locked by this process
valid = true
preNode, nextNode, prevPred *Node
)
// 如果可以执行删除操作,代码开始进行物理删除操作(从下到上)。首先,获取节点的前驱节点和后继节点,并加锁以确保操作的正确性。
for layer := 0; valid && (layer <= topLayer); layer++ {
preNode, nextNode = preNodes[layer], nextNodes[layer]
if preNode != prevPred { // the node in this layer could be locked by previous loop
preNode.mu.Lock()
highestLocked = layer
prevPred = preNode
}
// valid check if there is another node has inserted into the skip list in this layer
// during this process, or the previous is deleted by another process.
// It is valid if:
// 1. the previous node exists.
// 2. no another node has inserted into the skip list in this layer.
// 在有效性检查中,代码检查前驱节点和后继节点是否被标记,并且前驱节点的下一个节点是否为后继节点。
// 这些检查用于确保在删除节点过程中没有其他协程插入节点或删除前驱节点。如果检查失败,说明在此过程中有其他节点插入了跳表,代码需要释放已加的锁,并继续下一轮循环。
valid = !preNode.flags.Get(deletedMarked) && preNode.atomicLoadNext(layer) == nextNode
}
if !valid {
unlockordered(preNodes, highestLocked)
continue
}
// 如果有效性检查通过,代码开始进行物理删除操作。
for i := topLayer; i >= 0; i-- {
// Now we own the `nodeToDelete`, no other goroutine will modify it.
// So we don't need `nodeToDelete.loadNext`
// 在每个层级上,代码将前驱节点的下一个节点设置为要删除节点的下一个节点,从而将要删除节点从跳表中移除。
preNodes[i].atomicStoreNext(i, nodeToDelete.loadNext(i))
}
// 最后,释放已加的锁,并更新跳表的长度计数。
nodeToDelete.mu.Unlock()
unlockordered(preNodes, highestLocked)
atomic.AddInt64(&s.length, -1)
return true
}
return false
}
}
删除的逻辑与插入的逻辑大体相同,先调用findNodeDelete,如果没有找到则直接返回false,如果找到了则校验待删除节点状态是否为可删除状态(全链接,未被删除标记),如果校验通过,进行物理删除操作,在通过原子操作,从最高层开始将待删除节点的前驱节点的后继指针指向待删除节点的后继节点,最后释放锁,更新跳表长度
Len()
供外层调用的核心方法,用于获取跳表的元素数量
// Len returns the length of this skipmap.
func (s *ConcurrentSkipList) Len() int {
return int(atomic.LoadInt64(&s.length))
}
Range(…)
供外层调用的核心方法,用于获取跳表的元素数量
// Range calls f sequentially for each key and value present in the skipmap.
// If f returns false, range stops the iteration.
//
// Range does not necessarily correspond to any consistent snapshot of the Map's
// contents: no key will be visited more than once, but if the value for any key
// is stored or deleted concurrently, Range may reflect any mapping for that key
// from any point during the Range call.
func (s *ConcurrentSkipList) Range(f func(key any, value any) bool) {
x := s.header.atomicLoadNext(0)
for x != nil {
if !x.flags.MGet(fullyLinked|deletedMarked, fullyLinked) {
x = x.atomicLoadNext(0)
continue
}
if !f(x.key, x.loadVal()) {
break
}
x = x.atomicLoadNext(0)
}
}
从头节点开始遍历所有节点