第六次OJ练习Hint

Posted on by fxz

C – Mobile phones 【区间快速求和】

题目概述

指定一个S*S二维区域(可以理解为一个一个方格)，输入会有多种情形：

  • 1.指定对(x,y)的值加a（a可正可负）
  • 2.查询L<= X <= R , T<= Y <=B区域内所有方格的总和
  • 3.结束输入

知识点

树状数组/二元索引树（Binary Indexed Tree）
树状数组的英文表述为Binary Indexed Tree，但首先需要明确的是，它其实并不是一棵树。Binary Indexed Tree 事实上是将根据数字的二进制表示来对数组中的元素进行逻辑上的分层存储。他是用数组来实现的。
我们要解决特定区间求和的问题，最简单的算法无非就是一个数组存储，查询的时候计算这个范围内的元素和。但如果对于查询操作远远大于存储操作的情况，这种算法是非常低效的，因为会有大量的重复计算。树状数组的基本思想和线段树类似，他所存储的并不是原始数据，而是特定区域元素的和，查询量非常大时就可以大大减少重复计算。线段树的存储结构与数值的读取非常巧妙，篇幅及能力所限，证明过程此处不再详述。
Binary Indexed Tree 求和的基本思想在于，给定需要求和的位置i，例如 13，我们可以利用其二进制表示法来进行分段（或者说分层）求和：13 = 2^3 + 2^2 + 2^0，则prefixSum(13) = RANGESUM(1, 8) + RANGESUM(9, 12) + RANGESUM(13, 13)

 

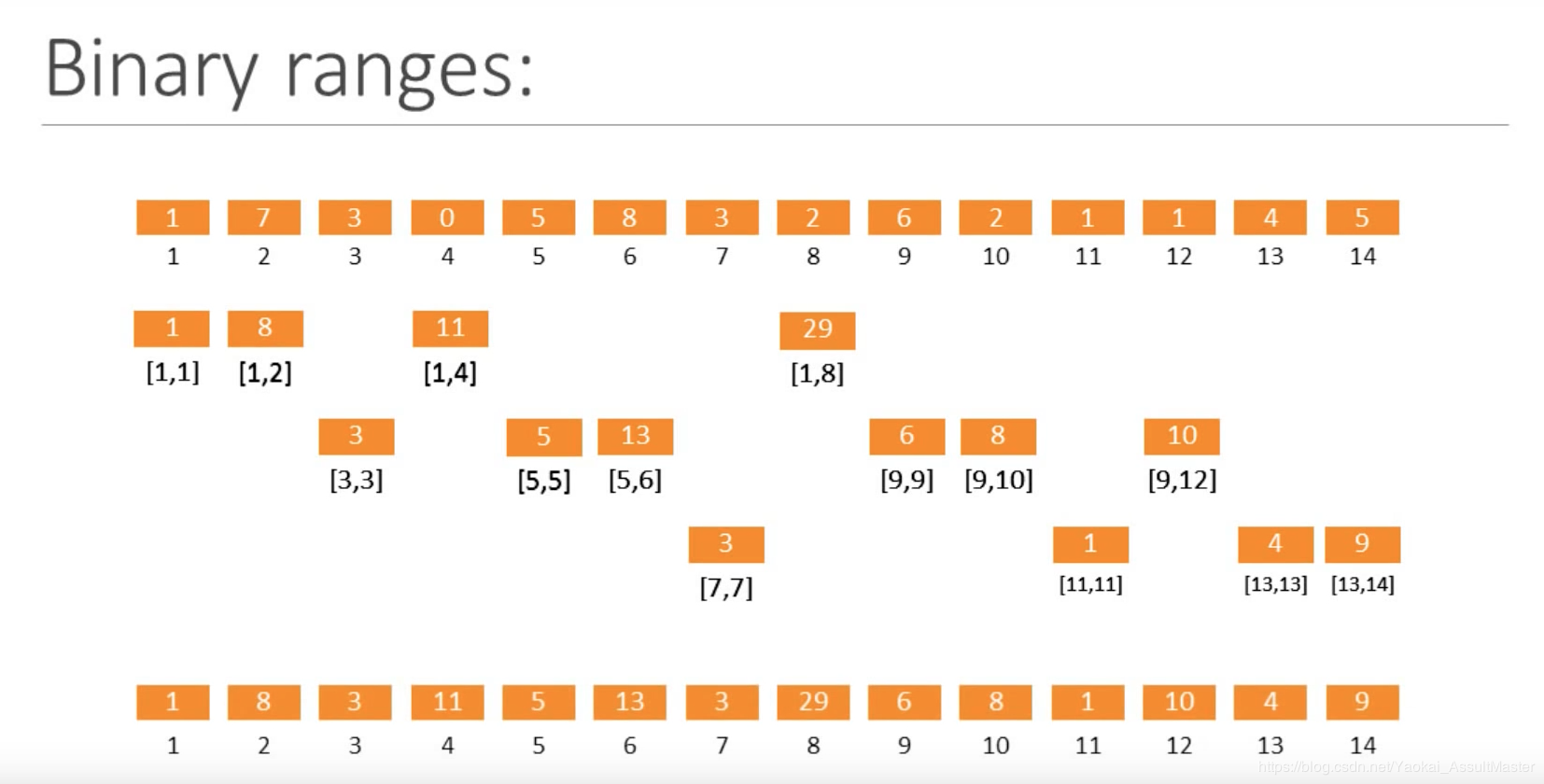
图中第一行为原数组，第二到第四行为依次按层填坑的过程。我们需要从左到右，从上到下依次将相应的值填入对应的位置中。最后一行中即为最终所形成的树状数组。

以图中第二行，也就是构造树状数组第一层的过程为例，我们首先需要填充的是数组中第一个数字开始，长度为__2 的指数__个数字的区间内的数字的累加和。所以图中分别填充了从第一个数字开始，长度为2^0, 2^1, 2^2, 2^3的区间的区间和。到此为止这一步就结束了。因为2^4超过了我们原数组的长度范围。

下一步我们构造数组的第二层。与上一层类似，我们依然填充余下的空白中从第空白处一个位置算起长度为__2 的指数__的区间的区间和。例如3-3空白，我们只需填充从位置 3 开始，长度为 1 的区间的和。再如9-14空白，我们需要填充从 9 开始，长度为2^0（9-9），2^1（9-10），2^2（9-12）的区间和。

类似地，第三层我们填充7-7，11-11和13-14区间的空白。

 

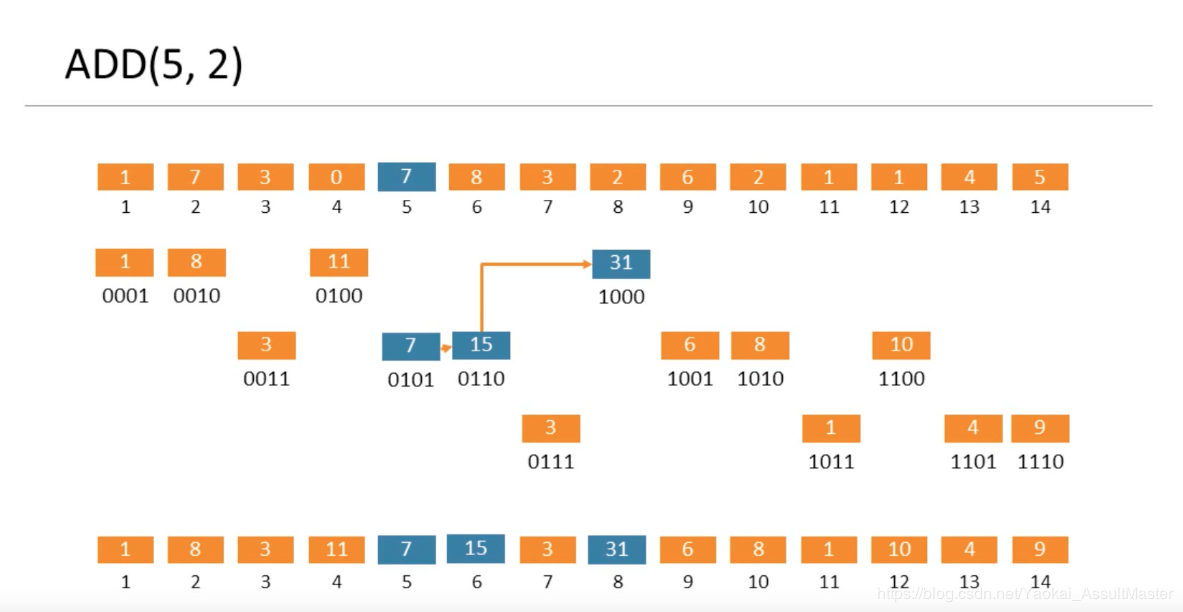
最后对树状数组的读取也用到了一个很巧妙的换算，是根据二进制位运算来的。

prefixSum(13) = prefixSum(0b00001101)
= BIT[13] + BIT[12] + BIT[8]
= BIT[0b00001101] + BIT[0b00001100] + BIT[0b00001000]

二进制的位运算（C语言中可以直接使用‘&’等位运算符）

x = 13 = 0b00001101
-x = -13 = 0b11110011
x & (-x) = 0b00000001
x – (x & (-x)) = 0b00001100

类似的更新数值的时候所应用的下标也是利用二进制位运算进行转换，不过是x + (x & (-x))

推荐阅读

解题思路

对于本题来说，直接套用树状数组是不可行的，因为是二维的区域，所以需要对原始数据进行两次处理。假设原数据存放在一个二维数组，那么第一次处理需要对每一行处理，将其转换树状数组的形式，第二次再对其列进行处理。

D – Balanced Lineup 【区间最值】

题目概述

给定一定长度的由整数组成的序列，查找出指定范围内的最值差值

知识点

RMQ (Range Minimum/Maximum Query) 区间最值查询
RMQ 问题是求给定区间中的最值问题。当然，最简单的算法是 O (n) 的，但是效率不够。可以用线段树将算法优化到 O（logn)（在线段树中保存线段的最值）。不过，Sparse_Table 算法才是最好的：它可以在 O (nlogn) 的预处理以后实现 O (1) 的查询效率。下面把 Sparse Table 算法分成预处理和查询两部分来说明 (以求最小值为例)。

  • 预处理:
    预处理使用 DP 的思想，f (i, j) 表示 [i, i+2^j – 1] 区间中的最小值，我们可以开辟一个数组专门来保存 f (i, j) 的值。
    例如，f (0, 0) 表示 [0,0] 之间的最小值，就是 num [0], f (0, 2) 表示 [0, 3] 之间的最小值，f (2, 4) 表示 [2, 17] 之间的最小值
    注意，因为 f (i, j) 可以由 f (i, j – 1) 和 f (i+2^(j-1), j-1) 导出，而递推的初值 (所有的 f (i, 0) = i) 都是已知的
    所以我们可以采用自底向上的算法递推地给出所有符合条件的 f (i, j) 的值。
  • 查询:
    假设要查询从 m 到 n 这一段的最小值，那么我们先求出一个最大的 k, 使得 k 满足 2^k <(n – m + 1).
    于是我们就可以把 [m, n] 分成两个 (部分重叠的) 长度为 2^k 的区间: [m, m+2^k-1], [n-2^k+1, n];
    而我们之前已经求出了 f (m, k) 为 [m, m+2^k-1] 的最小值，f (n-2^k+1, k) 为 [n-2^k+1, n] 的最小值
    我们只要返回其中更小的那个，就是我们想要的答案，这个算法的时间复杂度是 O (1) 的.
    例如，rmq (0, 11) = min (f (0, 3), f (4, 3))
    由此我们要注意的是预处理 f (i,j) 中的 j 值只需要计算 log (n+1)/log (2) 即可，而 i 值我们也只需要计算到 n-2^k+1 即可。

解题思路

本题需要查询区域内的两个最值，应用上述算法后，最后取差值输出即可。

E – Period 【字符串周期】

题目概述

在一个长度为N的字符串s中，判断他的长度为i的前缀字符串 s’是不是由一个最小子串s0连续重复K（K>1且尽可能大）构成的，如符合条件，则输出s’的长度i，以及子串重复的次数K。

知识点

KMP(Knuth-Morris-Pratt) 字符串查找算法
KMP算法是一个字符串匹配算法，其出发点是高效处理字符串匹配问题。朴素字符串匹配算法中，要在一个大的主字符串STR中查找目标小字符串string匹配位置的下标，其方法是对STR[i]逐个匹配string[0]，直到有一位STR[i0]==string[0],之后开始匹配string[1]……当出现有一位STR[i1]与string[j1]不匹配时，则后移一位从头开始匹配string，即开始判断STR[i1+1]与string[0]是否匹配。这样的运算是比较浪费的，KMP算法对此进行了优化。
KMP算法利用到了之前匹配失败的信息，匹配到失败的那一位之前，可以得知之前已经正确匹配了几位，利用这个信息，我们可以不用每次都在匹配到失败的一位后匹配STR[i1+1]与string[0]。具体实现可参阅下方链接。

推荐阅读

解题思路

本题可以利用KMP算法中的next数组快速求解

发表评论

您的电子邮箱地址不会被公开。